陳輝¹ ，鄭朋超² ，沈海波² ，武建龍¹ ，陳艷波²

( 1． 首鋼技術(shù)研究院; 2． 首鋼京唐鋼鐵聯(lián)合有限責(zé)任公司)

摘要：通過建立爐料在空區(qū)運動的數(shù)學(xué)模型，模擬研究了煤氣阻力對高爐布料的影響。通過研究認(rèn)為: 爐料在“空區(qū)”運動，是開爐或停風(fēng)測料面與理論布料模型間存在差別的原因之一，煤氣阻力是爐料在“空區(qū)”運動不同于靜態(tài)的拋物運動的根本原因; 煤氣阻力會使?fàn)t料沿水平、圓周切向的分速度均降低; 煤氣阻力的作用效果主要是促使?fàn)t料的主落點位置靠近高爐中心，在料線越深、布料傾角越大以及顆粒直徑越小時其作用效果越明顯; 隨著高爐冶煉強度的提高，煤氣所能吹出的最小顆粒直徑也迅速增大。

關(guān)鍵詞：高爐；煤氣阻力；布料

0 前言

目前大型高爐的布料設(shè)備基本上都采用料罐加溜槽的無鐘設(shè)備，溜槽布料靈活，可實現(xiàn)單環(huán)、多環(huán)、螺旋和定點布料，且設(shè)備密封性好，適應(yīng)了大型高爐的高頂壓操作。溜槽在布料的過程中，爐料的落點及形狀分布會受到爐料粒度、溜槽傾角、煤氣阻力以及科式力等眾多因素的影響。目前已經(jīng)有許多學(xué)者對高爐布料進(jìn)行了研究，其中包括建立顆粒運動及料流軌跡數(shù)學(xué)模型，實測高爐料流軌跡，以及研究爐頂設(shè)備參數(shù)等對高爐布料的影響^［1－5］。

通過實際高爐料流落點測定，焦炭與礦石的落點存在很大差異，即使相同的爐料顆粒由于粒徑不同，料流寬度變化也相當(dāng)大^［6］。這是由于顆粒出溜槽后在空區(qū)下降時，除受自身重力外還受煤氣浮力的作用，這些阻力隨顆粒的密度、粒徑、形狀等因素不同而變化，導(dǎo)致顆粒的落點也發(fā)生很大的偏差^［7］。

劉云彩研究認(rèn)為^［8］: 在一般冶煉條件下，煤氣阻力只相當(dāng)于直徑10 mm 粒度的礦石質(zhì)量的0．5%～8%，相當(dāng)于10 mm 焦炭質(zhì)量的1% ～ 2%; 但對于粒度在5 mm 以下的爐料，不容忽視。由于煤氣速度對布料作用的影響，在日常操作中，凡改變冶煉強度、富氧鼓風(fēng)、爐頂壓力等使煤氣體積發(fā)生變化的操作，均影響爐料分布，盡管這期間裝料制度不變，煤氣分布也會有變化。

高爐開爐實踐和實驗室的模擬實驗表明: 礦石在相同檔位和相同料線下的主落點位置一般有所差異，不同物理性質(zhì)下得到的結(jié)論是不一樣的。這就有力地說明了煤氣阻力對爐料在空區(qū)運動的影響，在開發(fā)無鐘布料模型時是應(yīng)該考慮煤氣阻力的影響。

以首鋼京唐1#高爐( 5 500 m³ ) 的物料條件和設(shè)備參數(shù)為基礎(chǔ)，模擬了在生產(chǎn)條件下，煤氣阻力對爐內(nèi)布料的影響，以期對高爐布料的調(diào)整提供參考。

1 爐料運動模型的建立及計算

固體顆粒在氣體和液體中運動過程中會受到氣體、液體對固體顆粒的阻力。前人的研究表明，固體顆粒在流體中運動時所受到的阻力可以用式( 1) 來計算:

式中: CD———阻力系數(shù);

A_P———等表面積球體的平均面積，m² ;

ρ_f———流體的密度，kg /m³ ;

w_s———固體和流體之間的相對速度，m/s;

F_D———流體阻力，N。

對于高爐實際布料過程而言，非規(guī)則的爐料顆粒在空區(qū)運動的過程中受到的煤氣阻力仍可以采用式( 1) 來計算，但是對于形狀不規(guī)則的固體顆粒其阻力系數(shù)CD 并不是一個固定的常數(shù)。1989 年，Haider 和Levenspiel 首先提出非規(guī)則顆粒的阻力系數(shù)與雷諾數(shù)和形狀系數(shù)的關(guān)系如式( 2) 所示:

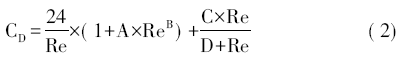
式中: R_e———顆粒的雷諾數(shù);

A～D———系數(shù)，并且是顆粒形狀系數(shù)的函數(shù)。

顆粒形狀系數(shù)的函數(shù)計算過程為:

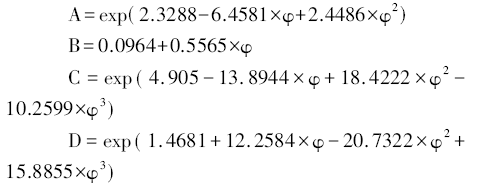
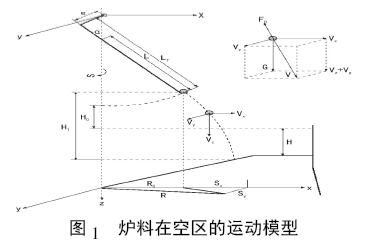
爐料以一定初速度進(jìn)入空區(qū)，在重力、浮力以及煤氣阻力的作用下，以斜拋運動的方式下降并最終落到料面上( 或者被煤氣帶走) 。由于煤氣阻力的作用導(dǎo)致不同的爐料種類和粒徑大小在空區(qū)的運動形式是不同的，大體可以分為以下三種類型: 爐料加速運動到達(dá)料面、爐料減速運動到達(dá)料面以及爐料被煤氣吹出。不同的運動類型導(dǎo)致爐料在空區(qū)的運動時間和落點位置是不一樣的。爐料在空區(qū)的運動形式如圖1 所示。

爐料在空區(qū)的運動方程如式( 3) 所示:

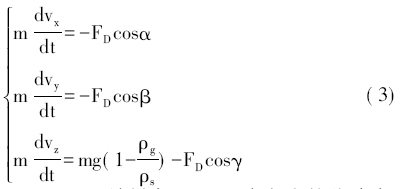
式中: v_x、v_y、v_z———爐料在X、Y、Z 方向上的分速度，m/s;

α、β、γ———爐料運動方向和X、Y、Z 的夾角，°;

ρ_g、ρ_s———煤氣的密度和爐料顆粒的視密度，kg /m³。

由于爐料顆粒在空區(qū)運動的過程中相對速度是不斷變化的，其大小的改變直接引起雷諾數(shù)R_e 變化，從而進(jìn)一步帶來煤氣阻力大小改變; 其方向的改變會引起煤氣阻力方向變化，即α、β、γ 發(fā)生變化，并直接影響爐料的最終落點位置( MSP) 。因此，計算爐料顆粒在整個空區(qū)的運動軌跡時，是必須考慮煤氣阻力的大小和方向的變化，而不能視為常數(shù)。料流運動軌跡子模型中采用原始料面逼近法計算爐料的最終主落點位置( MSP) 和其在空區(qū)的運動軌跡，其計算流程如圖2 所示。

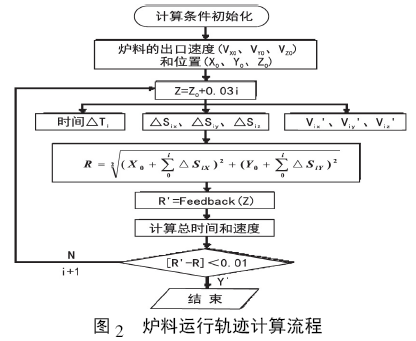
從圖2 可以看出，爐料在空區(qū)的下落過程中采用Z 方向的步進(jìn)法逐步向原始料面靠近，步進(jìn)量設(shè)定為0．03 m。在每次計算時，分別計算爐料在這一小段的通過時間以及位置和速度，從而得到爐料在空區(qū)的運動軌跡。由于原始料面對爐料主落點位置也會產(chǎn)生影響，所以程序在處理過程中加入Feedback(Z) 反饋程序，通過Z 方向的輸入給出原始料面在該處的半徑位置R’。最后比較R 和R’，當(dāng)兩者的絕對值相差0．01 m 時程序就認(rèn)為爐料已經(jīng)達(dá)到料面。

下面以焦炭為例，說明煤氣阻力對顆粒在空區(qū)運動以及最終落點的影響。計算所需焦炭的相關(guān)物性參數(shù)、裝料操作參數(shù)和部分設(shè)備參數(shù)分別見表1、表2。焦炭物性參數(shù)、裝料操作參數(shù)和設(shè)備參數(shù)均為首鋼京唐1#高爐實際生產(chǎn)數(shù)據(jù)。其中，煤氣流速度為1#高爐正常操作條件下爐頂煤氣的平均流速。

2 煤氣阻力影響焦炭分布的模擬結(jié)果

2．1 煤氣阻力和料線高度對焦炭主落點的影響

通過料流運動軌跡子模型計算，得到受煤氣阻力影響料線高度SL 與焦炭主落點位置MSP－coke的對應(yīng)關(guān)系，結(jié)果見表3 和圖3。

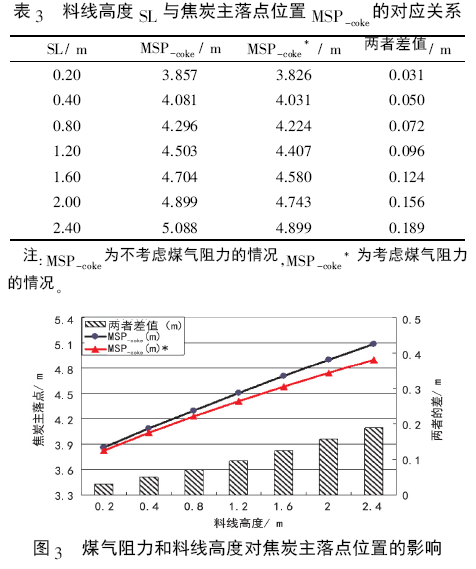
由表3 和圖3 可知，隨著料線高度的提高，焦炭主落點位置均增大，焦炭布向邊緣。但是由于煤氣阻力的作用使焦炭主落點位置比不考慮煤氣阻力時更小，焦炭更難布到邊緣; 此外需要注意的是，料線越深煤氣阻力對焦炭的落點半徑越明顯。這主要是因為煤氣阻力的存在使焦炭在空區(qū)的停留時間變長，與此同時焦炭在x、y 方向上做減速運動而并不是勻速運動，所以焦炭在空區(qū)下降的過程中，其在x、y 方向上發(fā)生的位移量減小，落點位置更靠近高爐中心。總體而言，由于煤氣阻力的作用使通過變料線操作來控制爐料主落點位置的效果降低。

2．2 煤氣阻力和顆粒直徑對焦炭主落點的影響

通過料流運動軌跡子模型計算，得到受煤氣阻力影響顆粒直徑Dp 與焦炭主落點位置MSP－coke的對應(yīng)關(guān)系，結(jié)果見表4 和圖4。

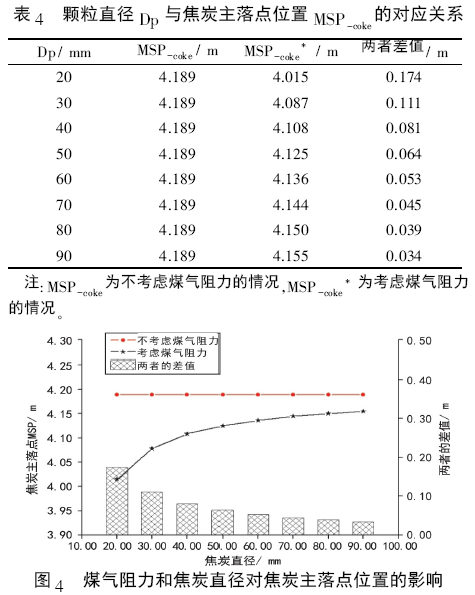
從表4 和圖4 可知，不考慮煤氣阻力的情況下，焦炭顆粒直徑的變化對其落點位置幾乎沒有影響。實際上，由于煤氣阻力的作用使大粒度更容易布向邊緣一側(cè)，而小粒度布向中心一側(cè)，而當(dāng)粒度越小煤氣阻力帶來的影響越大。由于小顆粒自身的重力小，而煤氣阻力與重力的比值( F /mg) 大，因此對其落點位置影響明顯。高爐實際裝入的爐料是粒度不同的顆粒組成的，其粒度組成情況對不同粒度的顆粒的落點位置影響較大，最直接的表現(xiàn)為料流寬度的變化。一般而言，爐料的粒度組成越不均勻，其料流寬度也越寬。

2．3 煤氣阻力和溜槽傾角對焦炭主落點的影響

通過料流運動軌跡子模型計算，的得到受煤氣阻力影響溜槽傾角CA 與焦炭主落點位置MSP－coke的對應(yīng)關(guān)系，結(jié)果見表5 和圖5。

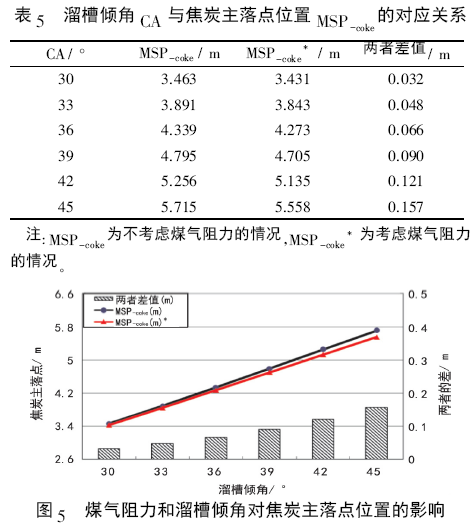
從表5 和圖5 可以看出，隨著溜槽傾角的增大，無論是否考慮煤氣阻力的影響焦炭主落點位置都是呈現(xiàn)增加的趨勢; 但是，考慮煤氣阻力的作用以后，焦炭主落點位置向高爐中心靠近，在溜槽傾角較大時這種趨勢越明顯。這主要有兩方面的原因，一是，溜槽傾角的增大帶來相同料線情況下，焦炭在空區(qū)的運動距離增大，帶來料線的變相增大; 二是，溜槽傾角變大帶來Z 方向速度的降低，煤氣阻力作用效果更大。

無鐘高爐開爐的重要任務(wù)之一就是制定檔位劃分方案，由于開爐過程中沒有上升的煤氣，因此實際布料檔位角度應(yīng)該在開爐實測布料檔位傾角的基礎(chǔ)上加上一個修正值，從而消除實際生產(chǎn)高爐和開爐時的爐況差異帶來的影響。

2．4 煤氣阻力對焦炭的上下臨界直徑的影響

焦炭從溜槽進(jìn)入空區(qū)以后，由于顆粒直徑大小的差異導(dǎo)致不同直徑顆粒在空區(qū)的運動形式是不一樣的。大體可以分為三種類型: 爐料加速運動到達(dá)料面、爐料減速運動到達(dá)料面以及爐料被煤氣吹出。因此，存在兩個臨界直徑來劃分不同的運動類型。其中以下臨界直徑表示顆粒能被吹出的最大直徑，與煤氣流速有關(guān); 上臨界直徑表示所有以加速運動的方式下降到料面的最小顆粒直徑，與顆粒進(jìn)入空區(qū)的初始速度和煤氣流速有關(guān)。不同煤氣流速下，焦炭的上下臨界直徑與煤氣流速的關(guān)系見表6 和圖6。

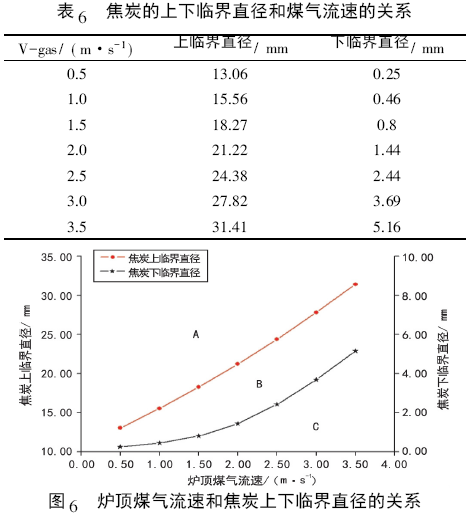
從表6 和圖6 可以看出，焦炭顆粒的上、下臨界直徑均隨煤氣平均流速的增大而增大。在煤氣平均流速為1．32 m/s 時，上臨界直徑為17．3 mm，下臨界直徑為0．68 mm。當(dāng)焦炭顆粒大于17．3 mm 時( 即A 區(qū)) ，其將以加速運動的方式下降到料面; 焦炭顆粒小于0．68 mm( 即C 區(qū)) ，其將會被煤氣吹出; 焦炭顆粒介于兩者之間時( 即B 區(qū)) ，其將以減速運動的方式下降到料面。對于A、B 區(qū)的焦炭來說，由于其速度變化后所受到的煤氣阻力也會變化，如果料線較深，其有可能最終以勻速的方式達(dá)到料面。

同時，計算了爐頂煤氣流速對燒結(jié)礦下臨界直徑的影響，并與焦炭下臨界直徑進(jìn)行了對比，如圖7所示。

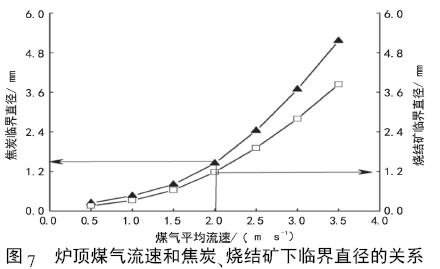
由圖7 可知，相同煤氣流速下，燒結(jié)礦的下臨界直徑低于焦炭，且焦炭和燒結(jié)礦臨界直徑的差隨煤氣流速的增加而增大。如煤氣流速為2 m/s 時( 工況條件下) ，焦炭的下臨界直徑為1．445 mm，而燒結(jié)礦的下臨界直徑為1．18 mm。爐料的下臨界直徑表征高爐冶煉條件下，隨煤氣進(jìn)入爐塵的顆粒大小，原料中含該臨界直徑的顆粒越多，則爐塵量可能增加。

對于實際生產(chǎn)高爐，爐頂料面以上的“空區(qū)”，煤氣流速在爐頂分布是不均勻的，這種不均勻性主要由裝料制度決定。一般而言，煤氣在中心以及邊緣的流速較快，因此在中心和邊緣區(qū)域其對應(yīng)的爐料的臨界直徑都更大。這意味著中心和邊緣區(qū)域可以將更大直徑的顆粒吹出，而這些顆粒會在煤氣流速低于平均流速的位置再次沉降下來，這將導(dǎo)致該區(qū)域的透氣性更差，促使煤氣分布向不均勻性方向發(fā)展。

另外，爐料所含的小顆粒爐料、粘附的小顆粒以及爐料下落沖擊新產(chǎn)生的顆粒，由于在爐頂料面以下的區(qū)域內(nèi)，煤氣流速高于“空區(qū)”，爐料的下臨界值會進(jìn)一步增大，甚至達(dá)到10 幾個毫米，進(jìn)入“空區(qū)”低煤氣流速區(qū)域再下落，進(jìn)一步會導(dǎo)致在爐喉料面間分布的均勻性變差，透氣區(qū)域更透氣、不透氣區(qū)域更不透氣。

3 結(jié)論

根據(jù)爐料在空區(qū)的受力和運動過程中實際情況，建立相應(yīng)的運動方程和數(shù)學(xué)模型，充分考慮了煤氣阻力對料流軌跡的影響，對爐料在“空區(qū)”的運動規(guī)律進(jìn)行了有意義的探索，豐富了無料鐘爐頂布料的理論內(nèi)涵，促進(jìn)了無料鐘爐頂裝料技術(shù)的完善。對爐料在空區(qū)的研究得到如下結(jié)論:

( 1) 爐料在“空區(qū)”運動，是開爐或停風(fēng)測料面與理論布料模型間存在差別的原因之一，煤氣阻力是爐料在“空區(qū)”運動不同于靜態(tài)的拋物運動的根本原因。

( 2) 煤氣阻力的作用使?fàn)t料沿水平、圓周切向的分速度均降低，其作用效果主要是促使?fàn)t料的主落點位置靠近高爐中心，在料線越深、布料傾角越大以及顆粒直徑越小時其作用效果越明顯，隨著高爐冶煉強度的提高，煤氣所能吹出的最小顆粒直徑也迅速增大。

( 3) 京唐1#高爐條件下，α = 36 °、料線1．6 m時，是否考慮“空區(qū)”煤氣阻力的作用，焦炭主落點遠(yuǎn)離爐墻、位置相差約0．12 m。

( 4) 京唐1#高爐條件下，焦炭的上臨界直徑為17．3 mm，下臨界直徑為0．68 mm。即當(dāng)焦炭顆粒大于17．3 mm 時，將以加速運動的方式下降到料面; 焦炭顆粒小于0．68 mm，其將會被煤氣吹出; 焦炭顆粒介于兩者之間時，其將以減速運動的方式下降到料面。

( 5) 同一煤氣流速條件下，燒結(jié)礦的下臨界直徑低于焦炭。

4 參考文獻(xiàn)

［1］ 郭其飛，李家新，楊佳龍，等． 大型高爐實用布料模型開發(fā)［J］．中國冶金， 2016，26( 12) : 17．

［2］ 曹偉，龍明華，高征鎧． 水鋼4#高爐開爐裝料實踐［J］． 中國冶金， 2013，23( 5) : 30．

［3］ 朱清天，程樹森，魏志江，等． 高爐爐料落點的確定［J］． 中國冶金， 2006，16( 9) : 24．

［4］ 許永華，吳敏，曹衛(wèi)華． 高爐布料的焦層坍塌建模方法研究［J］． 中國冶金， 2007，17( 6) : 30．

［5］ 嚴(yán)定鎏，郭培民，齊淵洪． 高爐內(nèi)爐料運動的數(shù)值模擬［J］． 中國冶金，2008，18( 4) : 21．

［6］ 鄭衛(wèi)國，李懷遠(yuǎn)，陳令坤，等． 武鋼1#高爐開爐裝料實測［J］．煉鐵，2002，21( 5) : 10．

［7］ 朱清天，程樹森． 高爐料流軌跡的數(shù)學(xué)模型［J］． 北京科技大學(xué)學(xué)報，2007，29( 9) : 932．

［8］ 劉云彩． 高爐布料規(guī)律［M］． 4 版． 北京: 冶金工業(yè)出版社，2012: 121．